선형 회귀와 경사 하강법 정리

January 13, 2022

저는 이 책을 참고하여 개념을 정리했습니다.

선형 회귀와 로지스틱 회귀

선형 회귀는 (x, y) 점들의 특징을 가장 잘 나타내는 선을 그리는 과정입니다.

독립변수 x 하나의 값만으로 y값을 설명할 수 있다면 단순 선형 회귀

여러개의 x값이 필요할 땐 다중 선형 회귀

최소 제곱법

최소 제곱법은 주어진 x의 값이 하나일 때 적용이 가능합니다. (단순 선형 회귀일 때)

여러개의 x가 주어지는 경우(다중 선형 회귀) 경사하강법을 적용합니다.

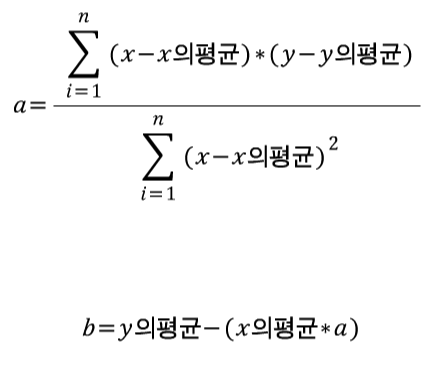
Alt text

최소제곱법을 이용하여 a, b 구하기

구하려는 직선이 y = ax + b라고 가정한다면,

a = (x - x평균) * (y - y평균)의 합 / (x - x평균)^2의 합

b = y - ax이므로

  = (y의 평균) - (a * x의 평균)

import numpy as np

x = [2, 4, 6, 8]
y = [81, 93, 91, 97]

mx = np.mean(x)  # x의 평균
my = np.mean(y)  # y의 평균

# 기울기 공식의 분모
divisor = sum([(i - mx)**2 for i in x])

# 기울기 공식의 분자
def top(x, y, mx, my):
    d = 0
    
    for i in range(len(x)):
        d += (x[i] - mx) * (y[i] - my)
    
    return d
divided = top(x, y, mx, my)

a = divided / divisor
b = my - mx * a

print(f"기울기 : {a}")
print(f"y절편 : {b}")

기울기 : 2.3
y절편 : 79.0

하지만, 모든 딥러닝 프로젝트는 여러개의 입력변수를 다룹니다.

따라서 최소제곱법이 아닌 다른 방법이 필요한데, 가장 많이 사용하는 방법은

'일단 그리고 조금씩 수정해 나가기' 방식입니다.

즉, 나중에 그린선이 먼저 그린 선보다 더 좋은지 나쁜지를 판단해야 하는데,

각 선의 오차를 계산하여 오차가 작은 쪽으로 바꾸는 알고리즘이 필요합니다.

평균 제곱 오차(MSE)

여러개의 x에 대해 오차가 존재하므로 모든 x에 대한 평균 오차를 평균 제곱 오차라고 합니다.

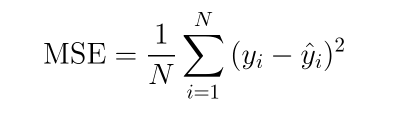
Alt text

따라서, 선형 회귀란 임의의 직선을 그어 이에 대한 평균 제곱 오차(MSE)를 구하고,

이 값을 가장 작게 만들어 주는 a와 b 값을 찾아가는 작업입니다.

# 위의 y = ax + b 활용

fake_a_b = [a, b]

# 위에서 구한 직선으로 y값 예측
def predict(x):
    return fake_a_b[0] * x + fake_a_b[1]

# MSE 함수
def mse(y, y_hat):  # y_hat: y의 평균
    return ((y - y_hat)**2).mean()

# MSE 함수를 각 y값에 대입하여 최종 값을 구하는 함수
def mse_val(y, predict_result):
    
    # 리스트의 각 원소끼리 -연산을 하기 위해 np.array형태
    return mse(np.array(y), np.array(predict_result))

# 예측값이 들어갈 리스트
predict_result = []

# 예측값 구하기
for i in range(len(x)):
    predict_result.append(predict(x[i]))
    print(f"x값 : {x[i]}, 실제 y값 : {y[i]}, 예측 y값 : {predict_result[i]}")
    
# 최종 MSE 출력
print(f"MSE : {mse_val(predict_result, y)}")

x값 : 2, 실제 y값 : 81, 예측 y값 : 83.6
x값 : 4, 실제 y값 : 93, 예측 y값 : 88.2
x값 : 6, 실제 y값 : 91, 예측 y값 : 92.8
x값 : 8, 실제 y값 : 97, 예측 y값 : 97.4
MSE : 8.299999999999985

오차 수정하기

기울기 a를 너무 크게 잡거나 너무 작게 잡으면 오차가 커집니다.

이러한 기울기 a와 오차의 관계는 이차 함수 그래프로 표현할 수 있습니다.

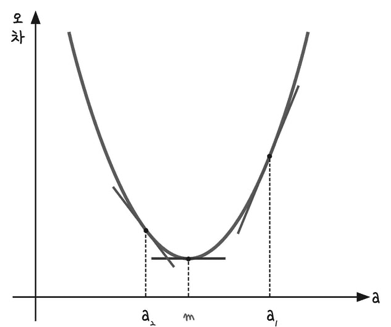
Alt text

오차가 가장 작을 때는 아래쪽의 볼록한 부분 m일때 입니다.

컴퓨터를 이용해 m의 값을 구하려면 임의의 한점(a1)을 찍고,

이점을 m에 가까운 쪽으로 점점 이동(a1 -> a2)시키는 과정이 필요합니다.

이러한 방법을 미분 기울기를 이용하는 경사 하강법이라고 합니다.

경사 하강법

최솟값 m에서의 순간 기울기는 0입니다.

즉, 경사 하강법에서는 미분값이 0인 지점을 찾는 것이 됩니다.

경사 하강법의 과정
1. a1에서 미분을 구합니다.
2. 구해진 기울기의 반대 방향(기울기가 +면 음의 방향, -면 양의 방향)으로
  
  이동시킨 a2에서 미분을 구합니다.
3. 구한 미분 값이 0이 될때까지 반복합니다.

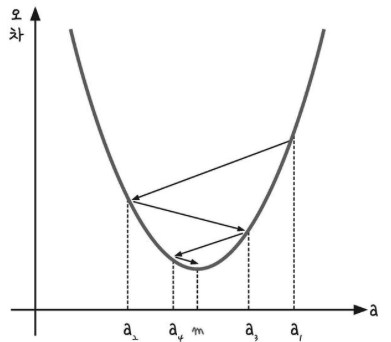
Alt text

학습률

기울기의 부호를 바꿔 이동시킬 때 적절한 거리를 찾지 못해 너무 멀리 이동시키면

a 값이 한점으로 모이지 않고 위로 치솟아 버립니다.

따라서 어느 만큼 이동시킬지를 신중히 결정해야 하는데, 이때 이동 거리를 정해주는 것이 바로 학습률입니다.

딥러닝에서 학습률의 값을 적절히 바꾸면서 최적의 학습률을 찾는 것은 중요한 최적화 과정 중 하나입니다.

따라서, 경사하강법은 오차의 변화에 따라 이차 함수 그래프를 만들고 적절한 학습률을 설정해

미분 값이 0인 지점을 구하는 것입니다.

y절편 b값(편향)도 이와 같은 성질을 가지고 있기 때문에 최적의 b값을 구할 때 역시 경사하강법을 사용합니다.

경사 하강법 실습

import pandas as pd
import matplotlib.pyplot as plt

# 그래프로 나타내기
plt.figure(figsize=(8, 5))
plt.scatter(x, y)
plt.show()

x_data = np.array(x)
y_data = np.array(y)

# 기울기 a와 절편 b의 값 초기화
a, b = 0, 0

lr = 0.03   # 적절한 학습률 정하기
epochs = 2001   # 몇 번 반복할지 설정

# 경사 하강법 시작
for i in range(epochs):
    y_pred = a * x_data + b    # y예측값 구하기
    error = y_data - y_pred
    
    # 오차 함수를 a로 미분한 값
    a_diff = -(2 / len(x_data)) * sum(x_data * error)
    
    # 오차 함수를 b로 미분한 값
    b_diff = -(2 / len(x_data)) * sum(error)
    
    a = a - lr * a_diff
    b = b - lr * b_diff
    
    if i % 100 == 0:  # 100번째 반복때마다 출력
        print(f"epochs = {i}, 기울기 = {a}, 절편 = {b}")
        
# 그래프 다시 그리기
y_pred = a * x_data + b
plt.scatter(x, y)
plt.plot([min(x_data), max(x_data)], [min(y_pred), max(y_pred)])
plt.show()

epochs = 0, 기울기 = 27.84, 절편 = 5.43
epochs = 100, 기울기 = 7.073858435872394, 절편 = 50.51166161138297
epochs = 200, 기울기 = 4.095999380762421, 절편 = 68.28224379060177
epochs = 300, 기울기 = 2.9756829100119027, 절편 = 74.96781336233505
epochs = 400, 기울기 = 2.5542024233262106, 절편 = 77.48302865233052
epochs = 500, 기울기 = 2.3956349066513707, 절편 = 78.42929177728175
epochs = 600, 기울기 = 2.3359793398132864, 절편 = 78.78529068727728
epochs = 700, 기울기 = 2.313535987420573, 절편 = 78.91922301600925
epochs = 800, 기울기 = 2.3050924490666174, 절편 = 78.96961044185792
epochs = 900, 기울기 = 2.3019158585694823, 절편 = 78.98856697541248
epochs = 1000, 기울기 = 2.3007207758016315, 절편 = 78.99569871827002
epochs = 1100, 기울기 = 2.300271167070735, 절편 = 78.99838179089187
epochs = 1200, 기울기 = 2.3001020172709508, 절편 = 78.9993912045567
epochs = 1300, 기울기 = 2.300038380484562, 절편 = 78.99977096168232
epochs = 1400, 기울기 = 2.3000144393354365, 절편 = 78.9999138322214
epochs = 1500, 기울기 = 2.3000054323026444, 절편 = 78.99996758234106
epochs = 1600, 기울기 = 2.300002043716771, 절편 = 78.99998780397235
epochs = 1700, 기울기 = 2.3000007688780433, 절편 = 78.99999541166466
epochs = 1800, 기울기 = 2.300000289263884, 절편 = 78.99999827379686
epochs = 1900, 기울기 = 2.3000001088255795, 절편 = 78.9999993505755
epochs = 2000, 기울기 = 2.3000000409418653, 절편 = 78.99999975567644

학습률 실습

# 경사하강법 구현
# 학습률을 여러가지 설정합니다.
lr_list = [0.001, 0.1, 0.5, 0.9]

def get_derivative(lr):
    w_old = 2
    derivative = [w_old]
    
    y = [w_old ** 2]  # 손실함수를 y = w^2
    
    for i in range(10):  # 미분값 구하기
        dev_value = w_old * 2
        
        # 미분값을 이용해서 가중치 업그레이드
        w_new = w_old - lr * dev_value
        w_old = w_new
        
        derivative.append(w_old) # 업데이트한 가중치를 저장
        y.append(w_old ** 2)  # 업데이트한 가중치의 손실값을 저장
    
    return derivative, y

x = np.linspace(-2, 2, 50)  # -2 ~ 2까지 50구간으로 나누기
x_square = [i ** 2 for i in x]

fig = plt.figure(figsize=(12, 7))

for i, lr in enumerate(lr_list):
    derivative, y = get_derivative(lr)
    ax = fig.add_subplot(2, 2, i + 1)
    ax.scatter(derivative, y, color = 'red')
    ax.plot(x, x_square)
    ax.title.set_text('lr = '+str(lr))
    
plt.show()

다중 선형 회귀

여러 독립 변수(x)가 존재하는 선형 회귀입니다.

data = [[2, 0, 81], [4, 4, 93], [6, 2, 91], [8, 3, 97]]  # [x1, x2, y]

# data로 부터 x1, x2, y의 리스트 만들기
x1 = [i[0] for i in data]
x2 = [i[1] for i in data]
y = [i[2] for i in data]

# 그래프로 확인(점 찍어보기)
ax = plt.axes(projection='3d')  # 3차원 그래프
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('y')
ax.dist = 11
ax.scatter(x1, x2, y)
plt.show()

# 리스트 -> numpy 배열
x1_data = np.array(x1)
x2_data = np.array(x2)
y_data = np.array(y)

a1, a2, b = 0, 0, 0  # 기울기 a1, a2와 절편 b 초기화
lr = 0.05  # 학습률
epochs = 2001  # 반복 횟수

for i in range(epochs):   # epochs만큼 반복
    y_pred = a1 * x1_data + a2 * x2_data + b
    error = y_data - y_pred    # 예측값에 대한 오차
    
    # 미분
    a1_diff = -(1 / len(x1_data)) * sum(x1_data * error)
    a2_diff = -(1 / len(x2_data)) * sum(x2_data * error)
    b_diff = -(1 / len(x1_data)) * sum(error)
    
    a1 = a1 - lr * a1_diff  # 학습률을 곱해 a1, a2, b값 업데이트
    a2 = a2 - lr * a2_diff
    b = b - lr * b_diff
    
    if i % 100 == 0:
        print(f"epochs = {i}, a1 = {a1}, a2 = {a2}, b = {b}")

epochs = 0, a1 = 23.200000000000003, a2 = 10.5625, b = 4.525
epochs = 100, a1 = 6.434805446608685, a2 = 3.98925524892891, b = 43.97569356791496
epochs = 200, a1 = 3.7255348759847924, a2 = 3.0541408134809784, b = 62.576629969168025
epochs = 300, a1 = 2.503714679287745, a2 = 2.6322742530634486, b = 70.96564181265175
epochs = 400, a1 = 1.952674645725859, a2 = 2.4420125981800993, b = 74.74908051776274
epochs = 500, a1 = 1.7041559609856545, a2 = 2.356204719590433, b = 76.45540883097016
epochs = 600, a1 = 1.592074201194008, a2 = 2.31750542401674, b = 77.22496175342586
epochs = 700, a1 = 1.5415254028566499, a2 = 2.300052067722291, b = 77.57202960424704
epochs = 800, a1 = 1.5187279287796718, a2 = 2.292180615763661, b = 77.7285569717077
epochs = 900, a1 = 1.5084462832928398, a2 = 2.28863059622062, b = 77.79915070923249
epochs = 1000, a1 = 1.5038092680884374, a2 = 2.2870295397926297, b = 77.83098843741102
epochs = 1100, a1 = 1.5017179773477205, a2 = 2.286307464419652, b = 77.84534723142188
epochs = 1200, a1 = 1.500774806629192, a2 = 2.285981808911738, b = 77.85182303787037
epochs = 1300, a1 = 1.5003494372690325, a2 = 2.28583493849654, b = 77.85474362222634
epochs = 1400, a1 = 1.5001575959734832, a2 = 2.2857687000379943, b = 77.85606080380799
epochs = 1500, a1 = 1.5000710756781244, a2 = 2.285738826537708, b = 77.85665485181606
epochs = 1600, a1 = 1.5000320550830635, a2 = 2.2857253536091546, b = 77.85692276706845
epochs = 1700, a1 = 1.500014456820917, a2 = 2.2857192773274324, b = 77.85704359666722
epochs = 1800, a1 = 1.5000065200165227, a2 = 2.285716536928462, b = 77.85709809073502
epochs = 1900, a1 = 1.500002940523069, a2 = 2.2857153010103657, b = 77.85712266752303
epochs = 2000, a1 = 1.5000013261739265, a2 = 2.2857147436121346, b = 77.85713375163787

로지스틱 회귀

참과 거짓(예/ 아니오)중에 하나를 내놓는 과정에서 사용하는 원리입니다.

참(1)과 거짓(0)사이를 구분하는 S자 형태입니다.

Sigmoid 함수

Sigmoid를 이용해 로지스틱 회귀를 풀어나갑니다.

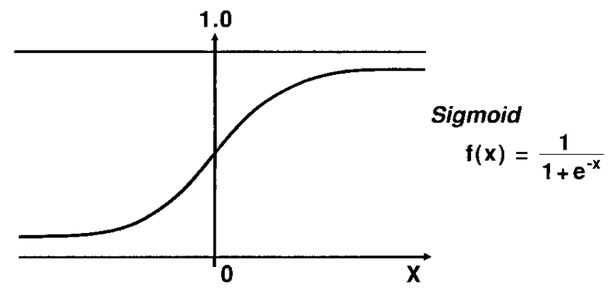
Alt text

지수부분이 (a * x + b)라고 했을 때,

a는 그래프의 경사도를 결정합니다. a값이 커지면 경사가 커지고 a값이 작아지면 경사가 작아집니다.

b는 그래의 좌우 이동을 의미합니다. b값이 크면 왼쪽, 작으면 오른쪽으로 이동합니다.

따라서, a와 b의 값에 따라 오차가 변합니다.

# sigmoid 구현

x_data = [2, 4, 6, 8, 10, 12, 14]
y_data = [0, 0, 0, 1, 1, 1, 1]

# 그래프로에 점 찍어보기
plt.scatter(x_data, y_data)
plt.xlim(0, 15)
plt.ylim(-0.1, 1.1)

a, b = 0, 0   # 기울기, 절편 초기화
lr = 0.05     # 학습률

def sigmoid(x):
    return 1 / (1 + np.e**(-x))

# 경사 하강법 실행
for epoch in range(2001):
    for i in range(len(x_data)):
        # 미분                 오차 : 예측값 - 실제값
        a_diff = x_data[i] * (sigmoid(a * x_data[i] + b) - y_data[i])
        b_diff = sigmoid(a * x_data[i] + b) - y_data[i]
        
        # a, b값 업데이트
        a -= lr * a_diff
        b -= lr * b_diff
        
        if epoch % 1000 == 0:
            print(f"epoch = {epoch}, 기울기 a = {a}, 절편 b = {b}")

epoch = 0, 기울기 a = -0.05, 절편 b = -0.025
epoch = 0, 기울기 a = -0.13879722189107602, 절편 b = -0.047199305472769
epoch = 0, 기울기 a = -0.2267516349901771, 절편 b = -0.06185837432261918
epoch = 0, 기울기 a = 0.12010284223274431, 절편 b = -0.018501564669754007
epoch = 0, 기울기 a = 0.23740192458962306, 절편 b = -0.006771656434066131
epoch = 0, 기울기 a = 0.27045811205658526, 절편 b = -0.004016974145152613
epoch = 0, 기울기 a = 0.2860409628939473, 절편 b = -0.0029039133710553225
epoch = 1000, 기울기 a = 1.497824502953391, 절편 b = -9.940123304992555
epoch = 1000, 기울기 a = 1.4940419536789271, 절편 b = -9.94106894231117
epoch = 1000, 기울기 a = 1.4119848217717417, 절편 b = -9.954745130962369
epoch = 1000, 기울기 a = 1.4949143121842228, 절편 b = -9.944378944660809
epoch = 1000, 기울기 a = 1.498244938547387, 절편 b = -9.944045882024492
epoch = 1000, 기울기 a = 1.4984392510394648, 절편 b = -9.94402968931682
epoch = 1000, 기울기 a = 1.4984505498747405, 절편 b = -9.944028882257157
epoch = 2000, 기울기 a = 1.9064689962225458, 절편 b = -12.948894836795326
epoch = 2000, 기울기 a = 1.9054981310086199, 절편 b = -12.949137553098806
epoch = 2000, 기울기 a = 1.8514893310246738, 절편 b = -12.958139019762797
epoch = 2000, 기울기 a = 1.9056614126778697, 절편 b = -12.951367509556148
epoch = 2000, 기울기 a = 1.9067744947792462, 절편 b = -12.95125620134601
epoch = 2000, 기울기 a = 1.9068037073321078, 절편 b = -12.951253766966605
epoch = 2000, 기울기 a = 1.9068044592233457, 절편 b = -12.951253713260089

Twitter Facebook LinkedIn

minyoongi96

선형 회귀와 경사 하강법 정리

선형 회귀와 로지스틱 회귀

최소 제곱법

최소제곱법을 이용하여 a, b 구하기

평균 제곱 오차(MSE)

오차 수정하기

경사 하강법

학습률

경사 하강법 실습

학습률 실습

다중 선형 회귀

로지스틱 회귀

Sigmoid 함수

공유하기

댓글남기기

참고

S3 CORS 테스트해보기

S3 버킷 정책 설정 & 암호화하기

S3 생성 & 퍼블릭 ACL 설정하여 외부 접근해보기

S3에 대한 기본 개념