다층 퍼셉트론(XOR문제)과 활성화 함수

저는 이 책을 참고하여 개념을 정리했습니다.

다층 퍼셉트론으로 XOR 문제 해결

• OR게이트와 NAND게이트, 이 두 가지를 내재한 각각의 퍼셉트론과

  AND게이트를 내제한 퍼셉트론을 사용해서 XOR문제를 해결합니다.

import numpy as np

w11 = np.array([-2, -2])   # NAND 게이트에 입력되는 가중치와 편향
b1 = 3
w12 = np.array([2, 2])     # OR
b2 = -1
w2 = np.array([1, 1])      # AND
b3 = -1

# 퍼셉트론 함수
def MLP(x, w, b):
    y = np.sum(w * x) + b
    if y <= 0:
        return 0
    else:
        return 1
    
def NAND(x1, x2):   # NAND 게이트
    return MLP(np.array([x1, x2]), w11, b1)

def OR(x1, x2):     # OR 게이트
    return MLP(np.array([x1,x2]), w12, b2)

def AND(x1, x2):    # AND 게이트
    return MLP(np.array([x1, x2]), w2, b3)

def XOR(x1, x2):
    return AND(NAND(x1, x2), OR(x1, x2))

if __name__ == "__main__":
    for x1, x2 in [(0, 0), (0, 1), (1, 0), (1, 1)]:
        y = XOR(x1, x2)
        print(f"입력값 : {(x1, x2)}, 출력값 : {y}")

입력값 : (0, 0), 출력값 : 0
입력값 : (0, 1), 출력값 : 1
입력값 : (1, 0), 출력값 : 1
입력값 : (1, 1), 출력값 : 0

• 퍼셉트론 하나로 해결되지 않던 문제를 은닉층을 만들어 해결했습니다.

• 은닉층을 여러개 쌓아올려 복잡한 문제를 해결하는 과정을 ‘신경망’이라고 부릅니다.

오차 역전파

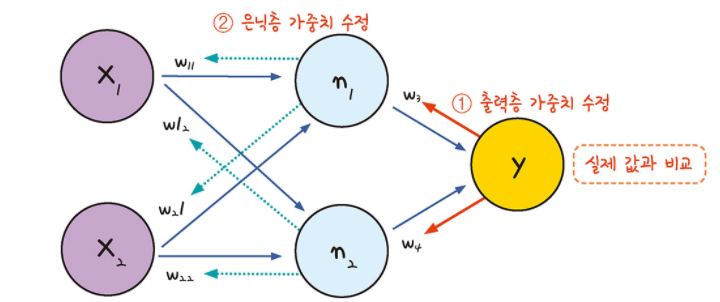
• 다층 퍼셉트론에서 결과값을 얻으면 오차를 구해 이를 토대로 앞선 가중치를 차례로 거슬러 올라가며 조정하는 작업

오차 역전파 과정

• 1. 결과 값과 실제 값을 비교하여 오차를 구합니다.
• 1. 경사 하강법을 이용해 바로 앞 가중치를 오차가 작아지는 방향으로 업데이트 합니다.
• 1. 위 과정을 더이상 오차가 줄어들지 않을 때까지 반복합니다.

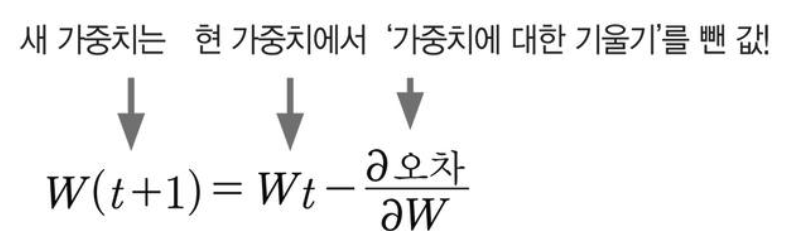
‘오차가 작아지는 방향으로 업데이트한다’는 의미는 미분 값이 0에 가까워지는 방향으로 나아간다는 말입니다.

가중치 수정 작업은 현 가중치에서 가중치에 대한 기울기를 뺀 값(즉, 미분 값)을 빼서 새 가중치로 조정합니다.

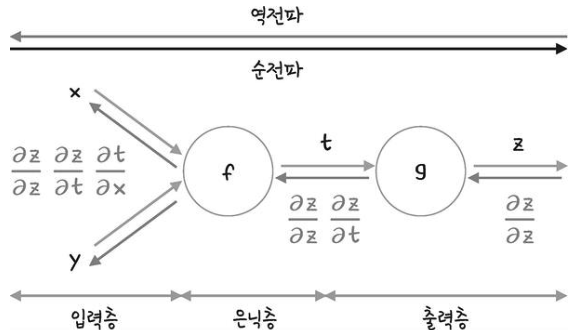
오차 역전파 과정에서 ‘체인룰’을 활용하여 미분 값을 얻어낼 수 있습니다.

기울기 소실 문제

은닉층이 늘어나면서 역전파를 통해 전달되는 기울기의 값이 점점 작아져

맨 처음 층까지 전달되지 않는 문제입니다.

이는 활성화 함수로 사용된 시그모이드 함수의 특성이 원인입니다.

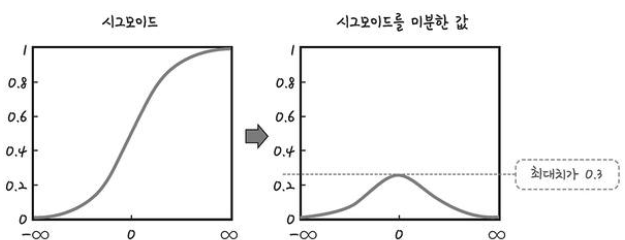
위 그림과 같이 시그모이드를 미분하면 최대값이 약 0.3이 됩니다.

1보다 작으므로 계속 곱하다 보면 0에 가까워지게 됩니다.

따라서, 여러 층을 거칠수록 기울기가 사라져 가중치를 수정하기가 어려워집니다.

이를 해결하고자 여러 활성화 함수로 대체합니다.

고급 경사 하강법

가중치를 업데이트하는 방법으로 경사 하강법이 존재합니다.

그런데 경사 하강법은 정확하게 가중치를 찾아가지만, 한 번 업데이트할 때마다 전체 데이터를

미분해야 하므로 계산량이 많아 속도가 느리고 최적해를 찾기 전에 멈출수 있다는 단점이 있습니다.

이러한 점을 보완하기 위해 고급 경사 하강법이 등장합니다.

확률적 경사 하강법(SGD)

확률적 경사 하강법은 전체 데이터를 사용하는 것이 아니라, 랜덤하게 추출한 일부 데이터를 사용합니다.

그러므로 더 빨리, 더 자주 업데이트를 하는 것이 가능합니다.

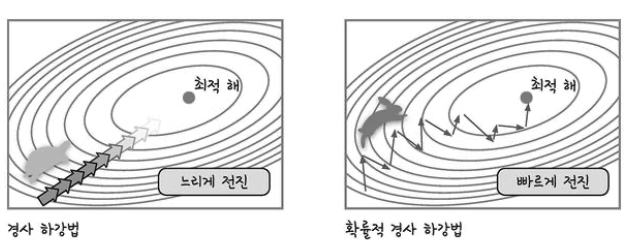
그림을 참고한다면, 랜덤한 일부 데이터를 사용하는 만큼 확률적 경사 하강법은

중간 결과의 진폭이 크고 불안정해 보일 수 있습니다.

하지만 속도가 확연히 빠르면서도 최적 해에 근사한 값을 찾아낼 수 있어 경사 하강법의 대안으로 사용되고 있습니다.

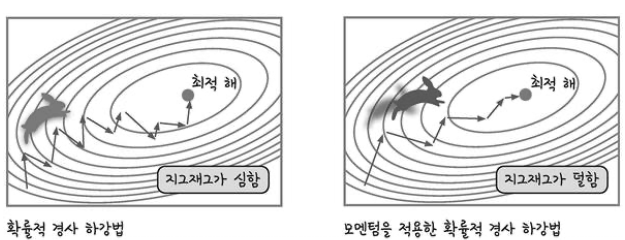
모멘텀(momentum)

momentum이란 ‘관성, 탄력, 가속도’라는 뜻입니다. 모멘텀 SGD란 말 그대로 경사 하강법에 탄력을 더한 것입니다.

경사 하강법과 마찬가지로 매번 기울기를 구하지만, 이를 통해 오차를 수정하기 전 바로 앞 수정값과

방향(+ / -)을 참고하여 같은 방향으로 일정한 비율만 수정되게 하는 방법입니다.

따라서 지그재그로 일어나느 현상이 줄어들고, 이전 이동 값을 고려해 일정 비율만큼만 다시 값을 결정하므로

관성 효과를 낼 수 있습니다.

고급 경사 하강법 활용법

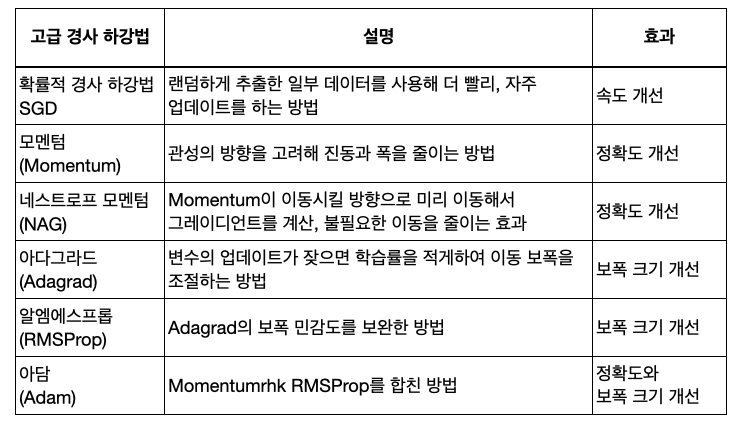
아담(Adam)은 현재 가장 많이 사용되는 고급 경사 하강법입니다.