minyoongi96

웹 개발 끄적끄적

MLP에서의 이미지 분석

  • MLP 신경망을 이미지 처리에 사용하면 이미지의 위치에 민감하게 동작하여 위치에 종속적인 결과를 얻게 됨
  • 이는 모든 픽셀을 연산하기 때문
  • MLP로 이미지 처리를 하기 위해서는 이미지를 1차원 벡터로 변환하고 입력층으로 사용해야 하는데, 이러면 공간적인 구조 정보가 유실되므로 좀 더 정확한 예측이 힘들다.

CNN (Convolution Neural Network)

  • MLP에서는 크기가 바뀌거나 이미지 데이터의 위치, 회전 정도가 다를 경우 특징 추출이 굉장히 힘들다.
  • 이러한 문제를 CNN으로 해결할 수 있다.

합성곱 신경망은 이미지 처리에 탁월한 성능을 보이는 신경망이고, 특성추출부와 MLP로 이루어져 있다.

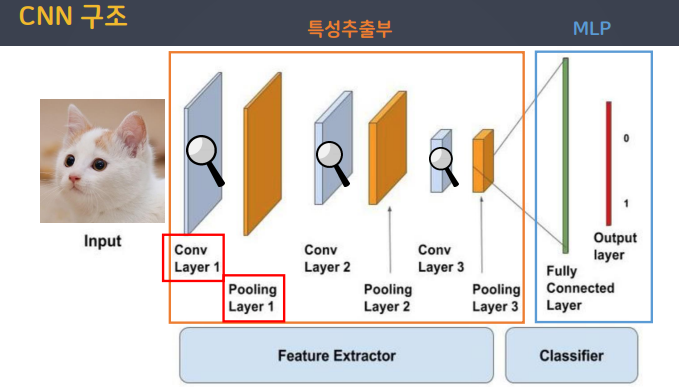
01_1.png

특성추출부

  • Convolution Layer(합성곱층)

    특징들을 부각해주는 역할을 함

  • Pooling Layer(풀링층)

    특징이 약한 부분을 없애주는 역할

Conv Layer는 특정 연산을 수행하기 때문에 뒤에 활성화 함수가 붙지만, Pooling Layer는 필요 없는 픽셀을 제거하는 역할만 수행하기 때문에 뒤에 활성화 함수가 오지 않는다.

채널

  • 합성곱 계층에서 이미지의 색상 정보를 채널이라고 부름
  • 이미지는 (높이, 너비, 채널)형태의 3차원 텐서
  • 흑백 이미지는 채널이 1, 컬러 이미지는(RGB) 3이다.

필터(=커널 = 가중치)

합성곱층은 합성곱 연산을 통해 이미지의 특징을 추출한다.

이때, 필터라는 N * M 크기의 행렬로 이미지를 처음부터 끝까지(가장 왼쪽 위 > 오른쪽 아래) 순차적으로 훑으면서(슬라이딩) 필터와 겹쳐지는 부분의 각 이미지와 필터의 원소(가중치) 값을 곱해서 모두 더한 값을 출력한다. 필터를 걸쳐 출력되는 데이터를 특성맵(feature map)이라고 한다.

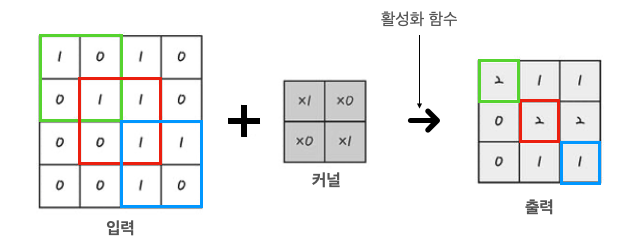
01_2.png

  • 그림 설명

    채널이 1인 (흑백 이미지) 2차원 합성곱일 경우 입력층에 필터를 지나쳐 출력 되는 예시이다.

    4x4크기 Input 이미지와 2x2크기 kernel을 합성곱 연산할 경우 3x3형태의 특성맵이 출력됨.

    물론, 필터에는 각 가중치가 존재하면서 편향도 존재한다.

    예를 들어, 편향이 +1 이라면 출력되는 특성맵의 각 원소들은 +1이 되어 출력된다.

여러개의 필터

Dense 층을 여러개를 사용하는 것처럼 여러개의 필터를 사용할 수 있고, 각 필터의 가중치도 서로 다르다.

여러개의 필터를 사용하면 특징 추출을 더 세밀하게 할 수 있다.

  • 채널 C개 입력 * 채널 C인 필터가 FN개 = 채널 FN개 출력
  • 즉, 출력 데이터의 채널 수 = 필터의 개수

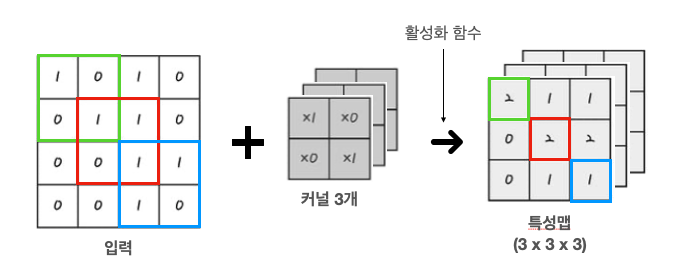
01_3.png

  • 우선 Input 이미지는 크기가 4X4인 상태이다.

    채널 1인 Input 이미지에 채널 1인 2X2 kernel 3개를 사용하면 3개의 3X3 크기의 특성맵을 얻을 수 있다.

    즉, 한 이미지의 특징을 추출한 부분을 3개로 세분화 시켰고, 이미지의 크기는 줄어들었다.

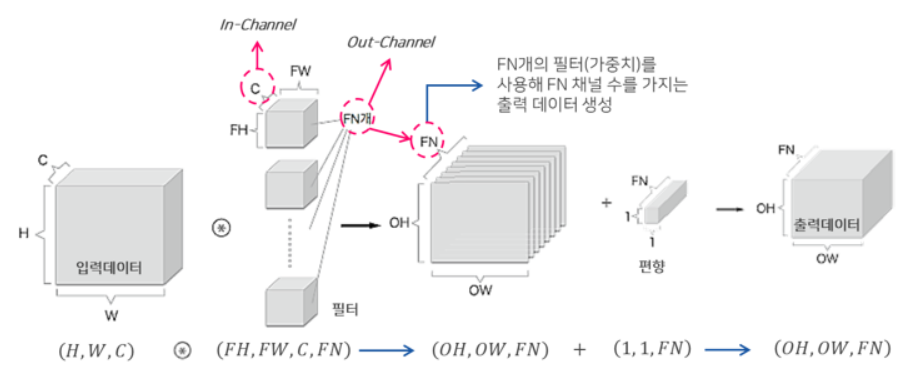
3차원 합성곱 정리

보통 컬러 이미지를 입력 데이터로 사용한다면 3차원 배열(높이, 너비, 채널(깊이)) 형태이다.

이러한 경우엔 커널도 동일한 채널을 갖게 된다.

(입력의 채널 수와 필터의 채널 수가 같아야함)

  • kernel의 채널(깊이)의 수 = Input 데이터의 채널(깊이)의 수
  • 합성곱 연산 결과 : Input 데이터는 채널 수와 상관없이 kernel 별로 1개의 특성맵이 만들어진다.즉, 입력 데이터의 깊이와 상관없이 (높이, 너비, 1)의 특성 맵을 얻음

  • 다만, 합성곱 연산에서 다수의 커널을 사용할 경우 : 특성 맵은 (높이, 너비, 커널의 수) 크기

    (특성 맵의 채널은 합성곱 연산에 사용된 커널의 수)

01_6.png

패딩(padding)

합성곱 연산을 수행하며 kernel을 통과할때마다 특성맵의 크기는 점점 줄어든다. 하지만, 복잡한 학습을 위해 깊은 층을 쌓아야 한다면 크기가 점점 줄어드는 탓에 더 이상 연산이 힘들어지게 된다.

그러므로, 여러 합성곱 연산 이후에도 특성맵의 크기를 비슷하게 유지되도록 패딩을 수행할 수 있다.

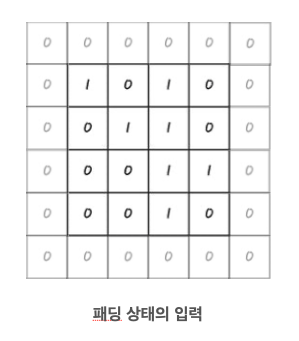
01_4.png

  • 입력 이미지의 가장 자리에 지정된 폭만큼 가상의 픽셀로 테두리를 추가한다.
  • 그렇다면 필터의 슬라이딩 범위가 늘어나게 되고 kernel에서 출력되는 특성맵의 크기는 패딩하기 전보다 커지게 된다.
  • 주로 0으로 채우기 대문에 제로 패딩(zero padding)이라고도 함

축소 샘플링

합성곱 수행 후 다음 계층으로 전달할 때, 모든 정보를 전달하지 않고 일부만 샘플링하여 넘겨주는 작업을 말한다. 크게 스트라이드(stride)와 풀링(pooling)이 있다.

스트라이드(stride)

그림에서는 kernel이 Input 이미지에 한 칸씩 이동(슬라이딩)하면서 합성곱 연산을 수행한다.

하지만, 커널의 슬리이딩 범위 또한 사용자가 정할 수 있다.

이러한 이동 범위를 스트라이드(stride)라고 한다.

  • kernel이 2픽셀. 3픽셀씩 건너 뛰면서 합성곱 연산을 수행하는 방법
  • stride2 또는 stride3이라고 하는데, 이렇게 하면 ouput 특성맵의 크기를 더 줄일 수 있다.

풀링(pooling)

일반적으로 합성곱 층(합성곱 연산 + 활성화 함수) 다음에는 풀링 층을 추가한다.

합성곱 층 ouput인 특성맵이 크고 복잡하다면 이를 축소(다운 샘플링)해야 한다. 이 과정을 풀링 연산이라 하며, 이러한 연산을 하는 층이 풀링 층이다.

  • 일반적으로 최대 풀링(max pooling)과 평균 풀링(average pooling)이 사용된다.
  • 최대 풀링은 지역 내 최대 값을 뽑아내는 방법이다.
  • 최대 풀링을 하면 지역 내의 대표 정보만 남기고 나머지 신호들을 제거하는 효과가 있음
  • 평균 풀링은 지역 내 평균 값을 뽑아내는 방법이다.

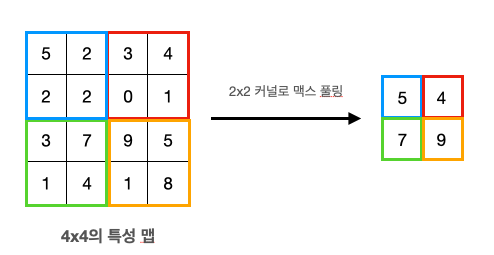
01_5.png

  • 2X2 Max Pooling 수행

    4X4 특성맵을 2X2 맥스 풀링하면 절반으로 특성맵이 작아지는 것을 확인할 수 있다.

    풀링은 통상적으로 2X2 풀링을 사용한다.

합성곱과 풀링의 차이

풀링도 합성곱 연산과 유사하게 커널을 슬라이딩 시켜 특성 맵을 얻으므로 유사한 느낌을 가질 수 있다.

하지만, 풀링은 합성곱 연산과 달리 곱하기나(가중치) 더하는(편향) 연산이 없고, 풀링 과정에서 커널이 슬라이딩할 때 서로 겹치지 않는다.

합성곱층 + 풀링층 사용

앞서 확인한 내용들을 바탕으로 컨볼루션 층과 풀링 층은 쌍으로 보통 사용한다.

(컨볼루션 층 + 풀링 층) 또는 (컨볼루션 층 + 컨볼루션 층 + 풀링 층) 이런 식으로 사용하게 되는데,

2차원 이상의 크기로 출력됨

그 후에 밀집층(은닉층+출력층 또는 출력층)을 사용하여 원하는 결과값을 얻기 위해 1차원 배열로 풀어서 펼치는 작업 수행, 따라서 Flatten을 사용하여 1차원 크기로 바꾸어 사용한다.

CNN 모델 만들기

from tensorflow.keras.layers import Conv2D, MaxPool2D, Flatten
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
  • Conv2D : 2D 이미지 데이터에 대해 특징이 되는 부분들을 부각시켜줌
    • input_shape : Input 데이터 크기(height, width, channel)
    • filters : 필터의 갯수
    • kernel_size : 필터의 크기
    • padding=‘same’ : 원본 데이터의 크기에 맞게 알아서 패딩 적용(valid : 적용X)
  • MaxPool2D : 2D 이미지 데이터에 대해 필요 없는 정보를 삭제(축소 샘플링)
    • pool_size : 디폴트 값은 2(2 X 2)
# 모델 설계
cnn_model = Sequential()

# 특성 추출부(Conv층)
cnn_model.add(Conv2D(input_shape=(224, 224, 3), filters=128, kernel_size=(3, 3), padding='same', activation='relu'))

# 특성 추출부(Pooling층)
cnn_model.add(MaxPool2D())
cnn_model.add(Conv2D(filters=256, kernel_size=(3, 3), padding='same', activation='relu'))
cnn_model.add(MaxPool2D())
cnn_model.add(Conv2D(filters=128, kernel_size=(3, 3), padding='same', activation='relu'))
cnn_model.add(MaxPool2D())
cnn_model.add(Conv2D(filters=64, kernel_size=(3, 3), padding='same', activation='relu'))cnn_model.add(MaxPool2D())

# 분류기(MLP)
cnn_model.add(Flatten())
cnn_model.add(Dense(128, activation='relu'))
cnn_model.add(Dense(64, activation='relu'))
cnn_model.add(Dense(32, activation='relu'))
cnn_model.add(Dense(3, activation='softmax'))
  • 생성한 CNN 모델 정보 확인하기
cnn_model.summary()

Model: "sequential_1"
_________________________________________________________________
 Layer (type)                Output Shape              Param #
=================================================================
 conv2d (Conv2D)             (None, 224, 224, 128)     3584

 max_pooling2d (MaxPooling2D  (None, 112, 112, 128)    0
 )

 conv2d_1 (Conv2D)           (None, 112, 112, 256)     295168

 max_pooling2d_1 (MaxPooling  (None, 56, 56, 256)      0
 2D)

 conv2d_2 (Conv2D)           (None, 56, 56, 128)       295040

 max_pooling2d_2 (MaxPooling  (None, 28, 28, 128)      0
 2D)

 conv2d_3 (Conv2D)           (None, 28, 28, 64)        73792

 max_pooling2d_3 (MaxPooling  (None, 14, 14, 64)       0
 2D)

 flatten_1 (Flatten)         (None, 12544)             0

 dense_5 (Dense)             (None, 128)               1605760

 dense_6 (Dense)             (None, 64)                8256

 dense_7 (Dense)             (None, 32)                2080

 dense_8 (Dense)             (None, 3)                 99

=================================================================
Total params: 2,283,779
Trainable params: 2,283,779
Non-trainable params: 0
_________________________________________________________________

댓글남기기

참고

S3 CORS 테스트해보기

S3에서 CORS를 적용하여 다른 Origin에서 접근을 하고자 한다면 Headers에 Cors정책을 추가해 주어야 한다.